تثليث زاوي

  ميّز عن تثليث زاوية.

  لمعانٍ أخرى، طالع تثليث (توضيح).

تستخدم عملية التثليث في إيجاد إحداثيات والبعد لسفينة بالنسبة للشاطئ وذلك بقياس الزوايا بين نقطتين مرجعيتين

عملية التثليث الزاوي أو التثليث في علم المثلثات والهندسة الرياضية هي عملية إيجاد إحداثيات والمسافة إلى نقطة بحساب طول ضلع مثلث باستخدام القياسات المأخوذة لزوايا وأضلاع المثلث المشكل من تلك النقطة ونقطتين مرجعيتين باستخدام قانون الجيب. يستخدم التثليث في العديد من التطبيقات منها المساحة والملاحة والفلك وتوجيه الصواريخ في العلوم العسكرية وغيرها.

الحساب

التثليث

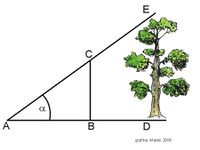
• الزاويتان α، β والمسافة AB معروفة مسبقاً
• من الممكن حساب C باستخدام المسافة RC أو MC
• RC من الممكن إيجاد موقع النقطة C من قانون الجيب

$\gamma =180^{\circ }-\alpha -\beta$

$\frac{\sin \alpha }{BC}=\frac{\sin \beta }{AC}=\frac{\sin \gamma }{AB}$

والأن نستطيع حساب AB وBC

$AC=\frac{AB\cdot \sin \beta }{\sin \gamma }$

$BC=\frac{AB\cdot \sin \alpha }{\sin \gamma }$

الخطوة الأخيرة هي حساب RC

$RC=AC\cdot \sin \alpha$

أو

$RC=BC\cdot \sin \beta$

وتعطى النتيجة بدلالة AB والزاويتين α وβ بإحدى الطريقتين

$RC=\frac{AB\cdot \sin \alpha \cdot \sin \beta }{\sin \gamma }=\frac{AB\cdot \sin \alpha \cdot \sin \beta }{\sin (180^{\circ }-\alpha -\beta )}=\frac{AB\cdot \sin \alpha \cdot \sin \beta }{\sin (\alpha +\beta )}$

• من الممكن حساب MC باستخدام قانون جيب التمام ومبرهنة فيثاغورس

$MR=AM-RB=\left(\frac{AB}{2}\right)-(BC\cdot \cos \beta )$

$MC=\sqrt{M{R}^2+R{C}^2}$

انظر أيضاً

• تثليث خطي
• تثليث السطح
• اختلاف المنظر